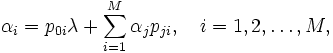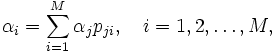ジャクソンネットワーク
【英】:Jackson network
目次 |
概要
各ノードはひとつまたは複数の窓口からなり, 指数分布にしたがうサービス時間でサービスを行い, ノードでのサービスを終えた客は次のノードまたは外部を確率的経路選択に したがって選ぶ待ち行列ネットワーク. 客をクラスにより区別しない. 外部からポアソン過程にしたがって客が到着する開放型と, 常に一定数の客が網内を循環している閉鎖型に分けられる. ネットワーク状態の定常確率分布は積形式をもつ. 基本的なモデルとして重要なものであり,広く応用されている.
詳説
ジャクソンネットワークの名は J.R.Jackson[5]に因る.1970年代後半から, 計算機システムの評価に応用されはじめた.待ち行列網の状態変化がマルコフ過程として記述され, 平衡方程式の解である定常確率分布が積形式として陽に表される基本的なモデルとして重要なものとなっている.
この待ち行列網の各ノードは指数分布に従うサービス時間をもつ窓口からなり, 1つのノードのサービスを終えた客が,その客の履歴によらず,経路選択確率と呼ぶ一定の確率で次のノードを選ぶモデルである.すなわち,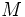 個のノード
個のノード からなり,ノード
からなり,ノード のサービス率はそのノードにいる客数
のサービス率はそのノードにいる客数 の関数で,
の関数で,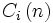 と表すことができる.例えば,ノード
と表すことができる.例えば,ノード のサーバー数が
のサーバー数が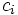 ,サービス時間分布がサービス率
,サービス時間分布がサービス率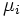 の指数分布ならば,
の指数分布ならば,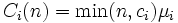 である.ノード
である.ノード のサービスを終えた客は経路選択確率
のサービスを終えた客は経路選択確率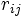 でノード
でノード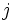 に移動する.
に移動する.
この網は,外部からの客の到着を仮定する開放型と,外部からの到着はなく,常に一定数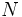 の客が網内を移動する閉鎖型に大別される.開放型の場合,外部からの到着過程は到着率
の客が網内を移動する閉鎖型に大別される.開放型の場合,外部からの到着過程は到着率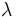 のポアソン過程とする.外部から到着した客は確率
のポアソン過程とする.外部から到着した客は確率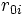 でノード
でノード に進み,ノード
に進み,ノード のサービスが終了した客は確率
のサービスが終了した客は確率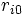 で網から退去する.少なくとも一つの
で網から退去する.少なくとも一つの について,
について,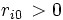 とならなければならない.閉鎖型の場合はすべての
とならなければならない.閉鎖型の場合はすべての について,
について,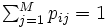 とする. 経路選択確率
とする. 経路選択確率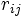 からなる正方行列を
からなる正方行列を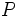 とする.開放型の場合,状態
とする.開放型の場合,状態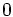 があるため,
があるため,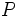 は
は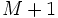 次となり,閉鎖型の場合
次となり,閉鎖型の場合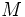 次となる.
次となる. 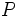 をマルコフ連鎖の推移確率行列とみたとき,既約であると仮定する.客のクラスが複数の場合の混合型 については,発展した型であるBCMP型やケリー型などのネットワークに分類される.また,外部からの到着があるが,系内に入ることができる客数に制限がある有限呼源(もしくは損失型)の場合,外部を一つのノードとみなすことにより,閉鎖型に帰着できる([5]参照).
をマルコフ連鎖の推移確率行列とみたとき,既約であると仮定する.客のクラスが複数の場合の混合型 については,発展した型であるBCMP型やケリー型などのネットワークに分類される.また,外部からの到着があるが,系内に入ることができる客数に制限がある有限呼源(もしくは損失型)の場合,外部を一つのノードとみなすことにより,閉鎖型に帰着できる([5]参照).
積形式解
この待ち行列網の状態を 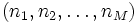 で表す. ここで
で表す. ここで 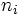 はノード
はノード  にいる客の数である. 定常状態確率を
にいる客の数である. 定常状態確率を 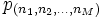 とすれば, これは次のような積形式になる.
とすれば, これは次のような積形式になる.
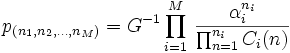
上記の積で 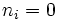 となる項は1とする.
となる項は1とする. 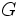 は正規化定数であり,
は正規化定数であり, 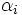
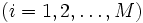 はトラフィック方程式と呼ばれるつぎの方程式の解である.
はトラフィック方程式と呼ばれるつぎの方程式の解である.
この方程式は,各ノード毎に到着率が退去率に等しいとして得られる1次の連立方程式である.開放型の場合,解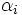 は一人の客が網に到着してから退去するまでにノード
は一人の客が網に到着してから退去するまでにノード を訪問する平均回数にネットワークへの総到着率
を訪問する平均回数にネットワークへの総到着率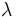 を乗じたものである.閉鎖型の場合は,トラヒック方程式は
を乗じたものである.閉鎖型の場合は,トラヒック方程式は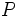 の定常確率を求める方程式と同一であり,さらに,例えば
の定常確率を求める方程式と同一であり,さらに,例えば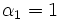 とすれば,
とすれば,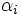 はノード1に到着してからまた次にそこに到着するまでの間にノード
はノード1に到着してからまた次にそこに到着するまでの間にノード を訪問する期待回数という意味をもつ.
を訪問する期待回数という意味をもつ.
定常分布が積形式となることから,開放型の場合,任意時点での,各ノードの列の長さは互いに独立になり,各ノードからの退去過程がポアソン過程になる.また,閉鎖型も含め,どんな部分ネットワークに対しても,部分ネットワーク全体を1つのノードで置き換えて,他の部分の定常分布が変えないようにすることができる. 長さは互いに独立になる.また,閉鎖型も含め,各ノードからの退去過程がポアソン過程になる.したがって,どんな部分ネットワークに対しても,部分ネットワー%ク全体を1つのノードで置き換えて,他の部分の定常分布が変えないようにすることができ, すなわち,ノートンの定理が任意の部分ネットワークに対して成り立つ[11].さらに,1つのノードへの各到着時点で,到着した客が見るネットワークの状態の分布は任意時点の状態分布と一致する.これを到着定理という.ただし,網が閉鎖型の場合には,任意時点の分布として,到着した客を除いた網を使う.さらにその客の退去時点での分布も同様であり[6],この分布でのもとで,ノード に到着してから,次にそこに戻るまでの平均周期時間はノードごとの平均訪問回数と平均待ち時間の積の総和となること等が求まる.
に到着してから,次にそこに戻るまでの平均周期時間はノードごとの平均訪問回数と平均待ち時間の積の総和となること等が求まる.
正規化定数と性能評価量の計算
積形式解から定常分布を求めるためには正規化定数の計算が必要である.開放型の場合は容易であるが,閉鎖型の場合には,可能な状態が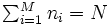 を満たすもに限られるので,工夫が必要である.例えば,閉鎖型正規化定数を計算する方法として,たたみ込み法や平均値解析法が知られている.[2].たたみこみ法では, ノード
を満たすもに限られるので,工夫が必要である.例えば,閉鎖型正規化定数を計算する方法として,たたみ込み法や平均値解析法が知られている.[2].たたみこみ法では, ノード  に対し,
に対し, 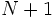 次元のベクトルを
次元のベクトルを
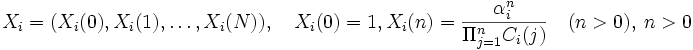
とし,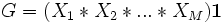 で与える.
で与える. はベクトルのたたみ込み演算である.定常分布が求まれば,スループットや平均待ち行列長の計算は比較的簡単である.しかし,正規化定数を計算することなく直接平均待ち行列長を計算する方法もある.例えば,平均値解析法は到着定理とLittleの公式を応用し,平均列長などを系内客数
はベクトルのたたみ込み演算である.定常分布が求まれば,スループットや平均待ち行列長の計算は比較的簡単である.しかし,正規化定数を計算することなく直接平均待ち行列長を計算する方法もある.例えば,平均値解析法は到着定理とLittleの公式を応用し,平均列長などを系内客数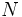 について0から繰り返し計算する方法である.各ノードでの平均待ち時間は到着時点での平均列長と平均サービス時間から求まる規律,例えば先着順であることが本質的である.
について0から繰り返し計算する方法である.各ノードでの平均待ち時間は到着時点での平均列長と平均サービス時間から求まる規律,例えば先着順であることが本質的である.
待ち時間
待ち時間の分布については,特殊な網について考察されている.開放型で,サーバー数が1のノード(規律は先着順)が直列に並んでいる網もJackson型の一つであるが,この網で一人の客の各ノードでの滞在時間は互いに独立であることがバークの定理として知られている[1],[9].これを閉鎖型にした場合,すなわち,最後のノードを退去した客は必ず最初のノードに戻る周期的な網でも,一周する間の一人の客の各ノードでの滞在時間の同時分布も一種の積の形となる[10].一人の客が他の客に追い越されることがない(overtake free)という性質が本質的であり,バークの定理は,この影響がない最初と最後のノードでのサーバー数が複数の場合でも成り立つ.特に最後のノードのサービス時間分布は任意でよい.その他,セントラルサーバモデルで規律がプロセッサシェアリングである場合の研究もある.(例えば[8]).
負の客とシグナル
ジャクソンネットワークの特徴は,ネットワーク内の各ノードに滞在する客数を要素とするベクトルを状態に取ると連続時間マルコフ連鎖により表されることにある.1990年代に[4]は,到着すると客数を減らす負の客という概念を導入し,同様なマルコフ連鎖によるモデル化を行い,ジャクソンネットワークと同様な積形式の定常分布をもつことを証明した.到着客が待ち行列に並んだ後にサービスを受けずに退去することがあるので,各ノードへの通常の客の総到着率は減少し,客の強制退去を考慮した非線形なトラヒック方程式の解として求められる.定常分布はこの変更された総到着率を使って表すことができる.その後,このモデルは,負の客が複数のノードを瞬間的に動き回るシグナル到着ネットワークへ拡張され,積形式の定常分布をもつことが証明されている([3]参照).例えば,各ノードで集団サービスが行われるジャクソン型と同様なネットワークで,予定された大きさの集団がサービスされた集団のみ1つの客となり経路を選択するモデルは,シグナル到着ジャクソンネットワークの例である.
集団移動型
ジャクソンネットワークと同様にポアソン到着やサービス時間が指数分布に従うモデルで,集団到着や集団退去があるモデルもあり,集団移動型と呼ばれる.このモデルは上記で述べた特別な場合を除いて,積形式の定常分布をもたないが,サービス集団の大きさがノードごとに独立であり経路の選択が集団ごとにまとめて行われる場合には,定常分布の補分布の上限を与える積形式分布が知られている(\[7],[12]参照).また,このモデルは,サービス完了時刻でネットワークの変化を追うと離散時間型のモデルと見なすこともできる.
参考文献
[1] P. J. Burke, "The Output Process of a Stationary M/M/s Queuing System, The Annals of Mathematical Statistics, 39 (1968), 1144-1152.
[2] K. M. Chandy and C. H. Sauer, "Computational Algorithms for Product Form Queueing Networks," Communications of the Association for Computing Machinery, 23 (1980), 573-583.
[3]X. Chao, M. Miyazawa and M. Pinedo, Queueing Networks; customers, signals and product form solutions, Wiley, 1999.
[4]E. Gelenbe, ``Product-form queueing networks with negative and positive customers, Journal of Applied Probability}, (1991), 656--663.
[5] J. R. Jackson, "Jobshop-like Queueing Systems," Management Science, 10 (1963), 131-142.
[6]T. Kawashima, ``A Property of two Palm measures in queueing networks and its applications,Journal of the Operations Research Society of Japan, (1982), 16--28.
[7]M. Miyazawa, P. Taylor, ``A geometric product-form distribution for a queueing network with nonstandard batch arrivals and batch transfers, Advances in Applied Probability 29, (1997), 523--544.
[8] J. A. Morrison and D. Mittra, "Heavy-usage Asymptotic Expansions for the Waiting Time in Closed Processor-sharing Systems with Multiple Casese," Advances in Applied Probability, 17 (1985), 163-185.
[9] E. Reich "Note on Queues in Tandem," The Annals of Mathematical Statistics, 34 (1963), 338-341.
[10] R. Schassberger and H. Daduna. "Sojourn Times in Queueing Networks with Multiserver Nodes," Journal of Applied Probability, 24 (1987), 511-521.
[11] J. Walrand, An Introduction to Queueing Networks, Prentice Hall, 1988.
[12]H. Yamashita, M. Miyazawa,``Product form queueing networks with concurrent movements, . Advances in Applied Probability, 30 (1998), 1111--1129.
ジャクソンネットワーク
【英】:Jackson network
目次 |
概要
各ノードはひとつまたは複数の窓口からなり, 指数分布にしたがうサービス時間でサービスを行い, ノードでのサービスを終えた客は次のノードまたは外部を確率的経路選択に したがって選ぶ待ち行列ネットワーク. 客をクラスにより区別しない. 外部からポアソン過程にしたがって客が到着する開放型と, 常に一定数の客が網内を循環している閉鎖型に分けられる. ネットワーク状態の定常確率分布は積形式をもつ. 基本的なモデルとして重要なものであり,広く応用されている.
詳説
ジャクソンネットワークの名は J.R.Jackson[5]に因る.1970年代後半から, 計算機システムの評価に応用されはじめた.待ち行列網の状態変化がマルコフ過程として記述され, 平衡方程式の解である定常確率分布が積形式として陽に表される基本的なモデルとして重要なものとなっている.
この待ち行列網の各ノードは指数分布に従うサービス時間をもつ窓口からなり, 1つのノードのサービスを終えた客が,その客の履歴によらず,経路選択確率と呼ぶ一定の確率で次のノードを選ぶモデルである.すなわち,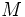 個のノード
個のノード からなり,ノード
からなり,ノード のサービス率はそのノードにいる客数
のサービス率はそのノードにいる客数 の関数で,
の関数で,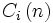 と表すことができる.例えば,ノード
と表すことができる.例えば,ノード のサーバー数が
のサーバー数が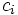 ,サービス時間分布がサービス率
,サービス時間分布がサービス率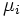 の指数分布ならば,
の指数分布ならば,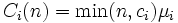 である.ノード
である.ノード のサービスを終えた客は経路選択確率
のサービスを終えた客は経路選択確率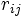 でノード
でノード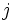 に移動する.
に移動する.
この網は,外部からの客の到着を仮定する開放型と,外部からの到着はなく,常に一定数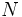 の客が網内を移動する閉鎖型に大別される.開放型の場合,外部からの到着過程は到着率
の客が網内を移動する閉鎖型に大別される.開放型の場合,外部からの到着過程は到着率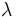 のポアソン過程とする.外部から到着した客は確率
のポアソン過程とする.外部から到着した客は確率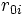 でノード
でノード に進み,ノード
に進み,ノード のサービスが終了した客は確率
のサービスが終了した客は確率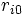 で網から退去する.少なくとも一つの
で網から退去する.少なくとも一つの について,
について,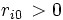 とならなければならない.閉鎖型の場合はすべての
とならなければならない.閉鎖型の場合はすべての について,
について,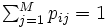 とする. 経路選択確率
とする. 経路選択確率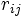 からなる正方行列を
からなる正方行列を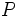 とする.開放型の場合,状態
とする.開放型の場合,状態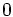 があるため,
があるため,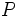 は
は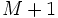 次となり,閉鎖型の場合
次となり,閉鎖型の場合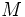 次となる.
次となる. 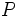 をマルコフ連鎖の推移確率行列とみたとき,既約であると仮定する.客のクラスが複数の場合の混合型 については,発展した型であるBCMP型やケリー型などのネットワークに分類される.また,外部からの到着があるが,系内に入ることができる客数に制限がある有限呼源(もしくは損失型)の場合,外部を一つのノードとみなすことにより,閉鎖型に帰着できる([5]参照).
をマルコフ連鎖の推移確率行列とみたとき,既約であると仮定する.客のクラスが複数の場合の混合型 については,発展した型であるBCMP型やケリー型などのネットワークに分類される.また,外部からの到着があるが,系内に入ることができる客数に制限がある有限呼源(もしくは損失型)の場合,外部を一つのノードとみなすことにより,閉鎖型に帰着できる([5]参照).
積形式解
この待ち行列網の状態を 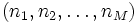 で表す. ここで
で表す. ここで 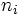 はノード
はノード  にいる客の数である. 定常状態確率を
にいる客の数である. 定常状態確率を 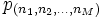 とすれば, これは次のような積形式になる.
とすれば, これは次のような積形式になる.
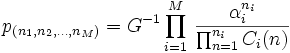
上記の積で 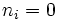 となる項は1とする.
となる項は1とする. 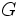 は正規化定数であり,
は正規化定数であり, 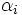
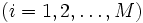 はトラフィック方程式と呼ばれるつぎの方程式の解である.
はトラフィック方程式と呼ばれるつぎの方程式の解である.
この方程式は,各ノード毎に到着率が退去率に等しいとして得られる1次の連立方程式である.開放型の場合,解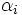 は一人の客が網に到着してから退去するまでにノード
は一人の客が網に到着してから退去するまでにノード を訪問する平均回数にネットワークへの総到着率
を訪問する平均回数にネットワークへの総到着率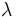 を乗じたものである.閉鎖型の場合は,トラヒック方程式は
を乗じたものである.閉鎖型の場合は,トラヒック方程式は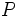 の定常確率を求める方程式と同一であり,さらに,例えば
の定常確率を求める方程式と同一であり,さらに,例えば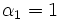 とすれば,
とすれば,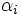 はノード1に到着してからまた次にそこに到着するまでの間にノード
はノード1に到着してからまた次にそこに到着するまでの間にノード を訪問する期待回数という意味をもつ.
を訪問する期待回数という意味をもつ.
定常分布が積形式となることから,開放型の場合,任意時点での,各ノードの列の長さは互いに独立になり,各ノードからの退去過程がポアソン過程になる.また,閉鎖型も含め,どんな部分ネットワークに対しても,部分ネットワーク全体を1つのノードで置き換えて,他の部分の定常分布が変えないようにすることができる. 長さは互いに独立になる.また,閉鎖型も含め,各ノードからの退去過程がポアソン過程になる.したがって,どんな部分ネットワークに対しても,部分ネットワー%ク全体を1つのノードで置き換えて,他の部分の定常分布が変えないようにすることができ, すなわち,ノートンの定理が任意の部分ネットワークに対して成り立つ[11].さらに,1つのノードへの各到着時点で,到着した客が見るネットワークの状態の分布は任意時点の状態分布と一致する.これを到着定理という.ただし,網が閉鎖型の場合には,任意時点の分布として,到着した客を除いた網を使う.さらにその客の退去時点での分布も同様であり[6],この分布でのもとで,ノード に到着してから,次にそこに戻るまでの平均周期時間はノードごとの平均訪問回数と平均待ち時間の積の総和となること等が求まる.
に到着してから,次にそこに戻るまでの平均周期時間はノードごとの平均訪問回数と平均待ち時間の積の総和となること等が求まる.
正規化定数と性能評価量の計算
積形式解から定常分布を求めるためには正規化定数の計算が必要である.開放型の場合は容易であるが,閉鎖型の場合には,可能な状態が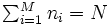 を満たすもに限られるので,工夫が必要である.例えば,閉鎖型正規化定数を計算する方法として,たたみ込み法や平均値解析法が知られている.[2].たたみこみ法では, ノード
を満たすもに限られるので,工夫が必要である.例えば,閉鎖型正規化定数を計算する方法として,たたみ込み法や平均値解析法が知られている.[2].たたみこみ法では, ノード  に対し,
に対し, 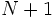 次元のベクトルを
次元のベクトルを
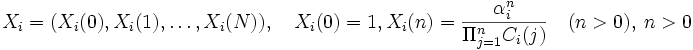
とし,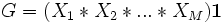 で与える.
で与える. はベクトルのたたみ込み演算である.定常分布が求まれば,スループットや平均待ち行列長の計算は比較的簡単である.しかし,正規化定数を計算することなく直接平均待ち行列長を計算する方法もある.例えば,平均値解析法は到着定理とLittleの公式を応用し,平均列長などを系内客数
はベクトルのたたみ込み演算である.定常分布が求まれば,スループットや平均待ち行列長の計算は比較的簡単である.しかし,正規化定数を計算することなく直接平均待ち行列長を計算する方法もある.例えば,平均値解析法は到着定理とLittleの公式を応用し,平均列長などを系内客数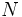 について0から繰り返し計算する方法である.各ノードでの平均待ち時間は到着時点での平均列長と平均サービス時間から求まる規律,例えば先着順であることが本質的である.
について0から繰り返し計算する方法である.各ノードでの平均待ち時間は到着時点での平均列長と平均サービス時間から求まる規律,例えば先着順であることが本質的である.
待ち時間
待ち時間の分布については,特殊な網について考察されている.開放型で,サーバー数が1のノード(規律は先着順)が直列に並んでいる網もJackson型の一つであるが,この網で一人の客の各ノードでの滞在時間は互いに独立であることがバークの定理として知られている[1],[9].これを閉鎖型にした場合,すなわち,最後のノードを退去した客は必ず最初のノードに戻る周期的な網でも,一周する間の一人の客の各ノードでの滞在時間の同時分布も一種の積の形となる[10].一人の客が他の客に追い越されることがない(overtake free)という性質が本質的であり,バークの定理は,この影響がない最初と最後のノードでのサーバー数が複数の場合でも成り立つ.特に最後のノードのサービス時間分布は任意でよい.その他,セントラルサーバモデルで規律がプロセッサシェアリングである場合の研究もある.(例えば[8]).
負の客とシグナル
ジャクソンネットワークの特徴は,ネットワーク内の各ノードに滞在する客数を要素とするベクトルを状態に取ると連続時間マルコフ連鎖により表されることにある.1990年代に[4]は,到着すると客数を減らす負の客という概念を導入し,同様なマルコフ連鎖によるモデル化を行い,ジャクソンネットワークと同様な積形式の定常分布をもつことを証明した.到着客が待ち行列に並んだ後にサービスを受けずに退去することがあるので,各ノードへの通常の客の総到着率は減少し,客の強制退去を考慮した非線形なトラヒック方程式の解として求められる.定常分布はこの変更された総到着率を使って表すことができる.その後,このモデルは,負の客が複数のノードを瞬間的に動き回るシグナル到着ネットワークへ拡張され,積形式の定常分布をもつことが証明されている([3]参照).例えば,各ノードで集団サービスが行われるジャクソン型と同様なネットワークで,予定された大きさの集団がサービスされた集団のみ1つの客となり経路を選択するモデルは,シグナル到着ジャクソンネットワークの例である.
集団移動型
ジャクソンネットワークと同様にポアソン到着やサービス時間が指数分布に従うモデルで,集団到着や集団退去があるモデルもあり,集団移動型と呼ばれる.このモデルは上記で述べた特別な場合を除いて,積形式の定常分布をもたないが,サービス集団の大きさがノードごとに独立であり経路の選択が集団ごとにまとめて行われる場合には,定常分布の補分布の上限を与える積形式分布が知られている(\[7],[12]参照).また,このモデルは,サービス完了時刻でネットワークの変化を追うと離散時間型のモデルと見なすこともできる.
参考文献
[1] P. J. Burke, "The Output Process of a Stationary M/M/s Queuing System, The Annals of Mathematical Statistics, 39 (1968), 1144-1152.
[2] K. M. Chandy and C. H. Sauer, "Computational Algorithms for Product Form Queueing Networks," Communications of the Association for Computing Machinery, 23 (1980), 573-583.
[3]X. Chao, M. Miyazawa and M. Pinedo, Queueing Networks; customers, signals and product form solutions, Wiley, 1999.
[4]E. Gelenbe, ``Product-form queueing networks with negative and positive customers, Journal of Applied Probability}, (1991), 656--663.
[5] J. R. Jackson, "Jobshop-like Queueing Systems," Management Science, 10 (1963), 131-142.
[6]T. Kawashima, ``A Property of two Palm measures in queueing networks and its applications,Journal of the Operations Research Society of Japan, (1982), 16--28.
[7]M. Miyazawa, P. Taylor, ``A geometric product-form distribution for a queueing network with nonstandard batch arrivals and batch transfers, Advances in Applied Probability 29, (1997), 523--544.
[8] J. A. Morrison and D. Mittra, "Heavy-usage Asymptotic Expansions for the Waiting Time in Closed Processor-sharing Systems with Multiple Casese," Advances in Applied Probability, 17 (1985), 163-185.
[9] E. Reich "Note on Queues in Tandem," The Annals of Mathematical Statistics, 34 (1963), 338-341.
[10] R. Schassberger and H. Daduna. "Sojourn Times in Queueing Networks with Multiserver Nodes," Journal of Applied Probability, 24 (1987), 511-521.
[11] J. Walrand, An Introduction to Queueing Networks, Prentice Hall, 1988.
[12]H. Yamashita, M. Miyazawa,``Product form queueing networks with concurrent movements, . Advances in Applied Probability, 30 (1998), 1111--1129.
| 待ち行列: | サービス率 サービス規律 ジャクソンネットワーク ジャクソンネットワーク タクシー乗り場モデル ダムモデル ハースト定数 |
| 待ち行列の応用: | アーラン, アグナー・K サービス品質 ジャクソンネットワーク ジャクソンネットワーク スループット トラヒック ネットワーク状態分布の正規化定数 |
| 待ち行列ネットワーク: | サービス規律 シグナル到着ネットワーク ジャクソンネットワーク ジャクソンネットワーク トラフィック方程式 ネットワーク状態分布の正規化定数 ノートンの定理 |
- ジャクソンネットワークのページへのリンク