パーフェクトグラフ
【英】:perfect graph
概要
グラフの頂点彩色を考えたときにクリークの各頂点は異なる色で塗らなければならない. すなわち, 任意のグラフに対して彩色数はクリーク数以上となる. 与えられたグラフ 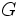 のすべての頂点誘導部分グラフに対して, その彩色数とクリーク数が等しいとき,
のすべての頂点誘導部分グラフに対して, その彩色数とクリーク数が等しいとき, 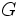 をパーフェクトグラフと呼ぶ. パーフェクトグラフの補グラフもパーフェクトグラフとなることが知られている.
をパーフェクトグラフと呼ぶ. パーフェクトグラフの補グラフもパーフェクトグラフとなることが知られている.
詳説
1960年代初頭にベルジュ (C. Berge) は, パーフェクトグラフ (perfect graph) の概念やそれに関する予想を提案した. 予想の一つ「パーフェクトグラフの補グラフもパーフェクトである」は, 1972年にロバース(L. Lovász) によって解かれた. それよりも強い予想であるパーフェクトグラフ予想 (perfect graph conjecture) (後述) は近年ついに証明された [3]. パーフェクトグラフは半正定値計画問題の研究の源流の一つでもあり, 計算の複雑さの観点からも興味深いグラフのクラスである. パーフェクトグラフに関しては参考文献にあげた図書 [1, 4] が詳しい.
与えられたグラフ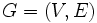 に対して, 集合
に対して, 集合 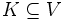 の任意の2頂点が隣接しているとき,
の任意の2頂点が隣接しているとき, 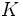 を
を 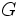 のクリーク (clique) とよぶ. 要素数最大のクリークを求める問題を
のクリーク (clique) とよぶ. 要素数最大のクリークを求める問題を 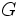 に対する最大クリーク問題 (maximum clique problem) とよぶ. 最大クリークの大きさをクリーク数 (clique number) といい,
に対する最大クリーク問題 (maximum clique problem) とよぶ. 最大クリークの大きさをクリーク数 (clique number) といい, 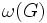 とかく. さらに, 頂点集合上の整数値重み
とかく. さらに, 頂点集合上の整数値重み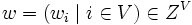 も導入し, 重みの総和を最大とするクリークを求める問題は次のような0-1整数計画問題
も導入し, 重みの総和を最大とするクリークを求める問題は次のような0-1整数計画問題
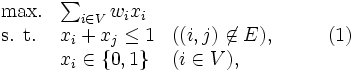
に定式化でき, この最適目的関数値を 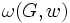 とかく. 明かに
とかく. 明かに 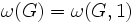 である. クリークと対称的な性質, 任意の2要素が互いに隣接しない集合
である. クリークと対称的な性質, 任意の2要素が互いに隣接しない集合 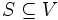 を
を 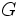 の安定集合 (stable set), あるいは独立集合 (independent set) という. 任意のクリークと安定集合の共通部分は高々1頂点であることを利用すると問題(1)は安定集合全体のなす族
の安定集合 (stable set), あるいは独立集合 (independent set) という. 任意のクリークと安定集合の共通部分は高々1頂点であることを利用すると問題(1)は安定集合全体のなす族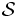 を用いて次のようにかける.
を用いて次のようにかける.
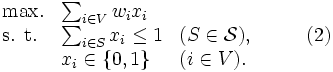
グラフ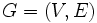 に対して, 隣接する頂点同士が異なる色になるような彩色の仕方を頂点彩色 (vertex coloring) あるいは単に彩色(coloring)とよぶ. 最小色数の頂点彩色を求める問題をグラフ彩色問題 (graph coloring problem) の一種である頂点彩色問題(vertex coloring problem) とよび, このときの最小色数を彩色数 (coloring number) といい,
に対して, 隣接する頂点同士が異なる色になるような彩色の仕方を頂点彩色 (vertex coloring) あるいは単に彩色(coloring)とよぶ. 最小色数の頂点彩色を求める問題をグラフ彩色問題 (graph coloring problem) の一種である頂点彩色問題(vertex coloring problem) とよび, このときの最小色数を彩色数 (coloring number) といい, 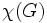 とかく. 彩色において同色の頂点の集合は安定集合であり, 頂点彩色問題は,
とかく. 彩色において同色の頂点の集合は安定集合であり, 頂点彩色問題は, 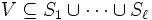 となる安定集合の族
となる安定集合の族 で最小のものを求める問題とみなせる. さらに, 頂点集合上の重み
で最小のものを求める問題とみなせる. さらに, 頂点集合上の重み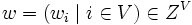 も導入し
も導入し
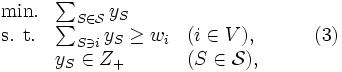
という問題の最適目的関数値を 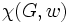 とかく(ただし
とかく(ただし は
は の安定集合全体のなす族,
の安定集合全体のなす族, 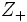 は非負整数全体を表す). 明かに
は非負整数全体を表す). 明かに 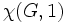 は彩色数
は彩色数 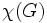 と一致する. 問題 (3) の整数条件
と一致する. 問題 (3) の整数条件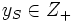 を非負条件
を非負条件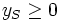 に置き換えた線形計画問題は, 問題 (2) の整数条件
に置き換えた線形計画問題は, 問題 (2) の整数条件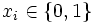 を非負条件
を非負条件 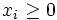 で置き換えた線形計画問題の双対問題である. このことから次の関係が示せる.
で置き換えた線形計画問題の双対問題である. このことから次の関係が示せる.
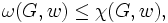
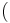 特別な場合として
特別な場合として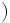
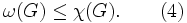
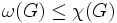 は任意の彩色でクリークの各頂点は異なる色に塗られることより明かであろう.
は任意の彩色でクリークの各頂点は異なる色に塗られることより明かであろう.
一般のグラフに対する最大クリーク問題や頂点彩色問題のNP困難性が知られている. すなわち, 多くの研究者はこれらの問題に対する多項式時間解法は存在しないと信じている. 不等式 (4) の間に入る量で多項式時間で計算出来るものにロバース数 (Lovász number)がある. (本来の定義とは異なるが) ロバース数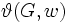 は
は
|
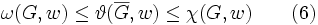
が成立する. グレッチェル (M. Grötschel), ロバースとシュライバー (A. Schrijver) は楕円体法でロバース数を多項式時間で求められることを示した. また (5) は半正定値計画問題なので, 半正定値計画問題に対する多項式時間解法でロバース数を求めることができる.
グラフ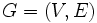 と
と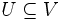 に対して, 頂点集合を
に対して, 頂点集合を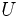 とし, 両端点が
とし, 両端点が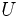 に含まれる辺全体を辺集合とする
に含まれる辺全体を辺集合とする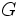 の部分グラフを,
の部分グラフを, 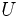 に誘導される頂点誘導部分グラフとよぶ.
に誘導される頂点誘導部分グラフとよぶ. 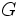 のすべての頂点誘導部分グラフ
のすべての頂点誘導部分グラフ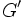 に対して
に対して 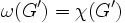 を満たすグラフをパーフェクトグラフ (perfect graph) という. パーフェクトグラフを特徴付ける性質として次のようなものがある.
を満たすグラフをパーフェクトグラフ (perfect graph) という. パーフェクトグラフを特徴付ける性質として次のようなものがある.
(c) 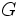 のクリークの特性ベクトル全体の凸包が, 非負条件と問題 (2) の安定集合による不等式で表現できる,
のクリークの特性ベクトル全体の凸包が, 非負条件と問題 (2) の安定集合による不等式で表現できる,
(d) 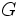 の任意の頂点誘導部分グラフ
の任意の頂点誘導部分グラフ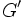 に対して
に対して 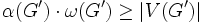 が成立する, ただし
が成立する, ただし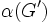 は
は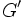 の最大安定集合の要素数,
の最大安定集合の要素数, 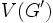 は
は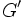 の頂点集合を表す,
の頂点集合を表す,
(e) 頂点誘導部分グラフとして長さ5以上の奇ホールもその補グラフも含まない.
(a) と (b) よりパーフェクトグラフに対して (6) は等号で成り立ち, 補グラフのロバース数を求めることで最大クリーク問題や頂点彩色問題が多項式時間で解けることが分かる. (c) は凸多面体を用いた特徴付けを与えている. (d) はロバースの与えた特徴付けで, この特徴付けより, 与えられたグラフがパーフェクトであるかの判定問題はco-NPに属する事が導かれる. この判定問題は多項式時間で解くことができる [2] (e) がパーフェクトグラフ予想と呼ばれていたものであり, 論文 [3] において証明され, 現在は強パーフェクトグラフ定理 (Strong Perfect Graph Theorem) と呼ばれる.
[1] J. L. Ramírez-Alfonsín and B. A. Reed, eds., Perfect Graphs, John Wiley & Sons, 2001.
[2] M. Chudnovsky, G. Cornuéjols, X. Liu, P. Seymour and K. Vuskovic, "Recognizing Berge Graphs," Combinatorica, 25 (2005), 143-186.
[3] M. Chudnovsky, N. Robertson, P. Seymour and R. Thomas, "The Strong Perfect Graph Theorem," Ann. of Math., 164 (2006), 51-229.
[4] M. Grötschel, L. Lovász and A. Schrijver, Geometric Algorithms and Combinatorial Optimization, Springer-Verlag, 1988.
| 組合せ最適化: | ナップサック問題 ネットワークフロー問題 ハッシュ表 パーフェクトグラフ パーフェクトグラフ予想 ヒープ ファセット制約 |
ぱーふぇくとぐらふと同じ種類の言葉
- ぱーふぇくとぐらふのページへのリンク
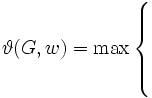
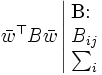
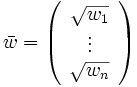
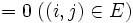
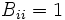
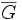 と表すと,
と表すと, 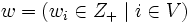
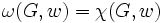 ,
,