効用関数
【英】:utility function
概要
任意の2つの選択対象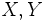 に対し,
に対し, 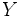 よりも
よりも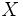 を好むことを表す選好関係
を好むことを表す選好関係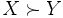 が数の大小関係
が数の大小関係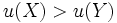 と同値となるような実数値関数
と同値となるような実数値関数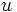 を,
を, 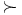 を表現する効用関数という. また, 貨幣のように譲渡可能な財があって,その
を表現する効用関数という. また, 貨幣のように譲渡可能な財があって,その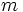 単位と
単位と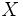 との組
との組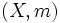 の効用が
の効用が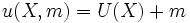 と与えられるとき,
と与えられるとき,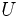 を譲渡可能効用という. さらに,
を譲渡可能効用という. さらに, 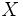 がくじで
がくじで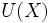 が
が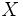 の期待効用として与えられるとき,
の期待効用として与えられるとき, 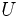 は譲渡可能なフォンノイマン・モルゲンシュテルン効用となる.
は譲渡可能なフォンノイマン・モルゲンシュテルン効用となる.
詳説
自然科学の領域で「価値」が陽に議論されることは少ないが, 人間を主体にした方策を論じるオペレーションズ・リサーチの分野では「価値」の問題を避けて通ることはできない.
効用関数とは, 一言でいえば人間の価値観を定量的に表現するための数学モデルである. 価値に関する科学的アプローチは経済学の分野で古くから扱われてきた. 人びとは財を消費したりサービス受けることによって一定の心理的満足感を得るが, この満足の度合いを効用という. この概念は消費者行動理論において基本的役割を担う [1].
いま, 財Aを 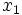 量, 財Bを
量, 財Bを 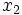 量だけ消費するときに得られる効用(または価値)を
量だけ消費するときに得られる効用(または価値)を 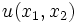 で表し, これを効用関数(または価値関数)という. ここで予算
で表し, これを効用関数(または価値関数)という. ここで予算 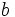 が与えられたとして, 財A, Bの単位量あたりの価格をそれぞれ
が与えられたとして, 財A, Bの単位量あたりの価格をそれぞれ 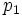 ,
, 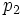 とすれば, 消費者は
とすれば, 消費者は

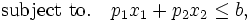
を満たす解, すなわち予算制約のもとで最も大きい満足感が得られる財Aと財Bの量の組を購入するであろう. すなわち, 「消費者は自己の効用を最大にする行動をとる」と考えて消費者行動を説明することが試みられている.
近代経済学の初期においては, 主観価値説として基数尺度 (cardinal scale)に従う基数効用関数(cardinal utility function)の存在を仮定することによってさまざまな経済理論を展開した. それは限界効用(marginal utility)を中心にした議論で限界革命とも呼ばれている. しかし, その後, 効用の可測性はあまりにも強い要請であると批判され, 人びとの主観的価値を表現する効用関数として基数効用関数を排除し, 大きさの大小関係だけを表す順序尺度 (ordinalscale)に従う序数効用関数(または順序効用関数)(ordinal utility function)のみの存在を仮定することによって経済分析を行う方向に移ってゆく [1]. これは, 経験的に与えられる無差別曲線(indifference curve)を使って消費者行動を説明しようとするパレートの提案によるものである. 無差別曲線から導かれる序数効用に対して限界効用(効用の微分値)の概念は使えない. そのかわりに無差別曲線の傾きを表す限界代替率(marginal rate of substitution)が使われる [2].
消費者行動の均衡条件を導出するうえでは序数効用関数によってその目的を達成することができるが, 多目的意思決定(multiple criteria decision making)のための選好解を導出するには, 基数効用関数の存在を仮定することが必要になる. さらに, リスクを伴う意思決定問題では, 評価の対象となる結果がある確率分布のもとで発生するので, 選好順序を求めるうえで効用の期待値を評価する必要があり, そのためには基数効用関数が必要になる. リスク下の意思決定問題に対して期待効用最大化の仮説が意味をもつように,公理系をはじめて作ったのはフォン・ノイマンとモルゲンシュテルンである [3].
結果の集合 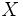 上の基数効用関数
上の基数効用関数 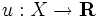 の,
の, 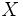 上の確率についての期待値
上の確率についての期待値
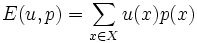
を期待効用(expected utility)という. 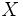 上の確率の集合を
上の確率の集合を 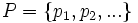 とするとき, 期待効用の大小によって
とするとき, 期待効用の大小によって 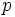 上の選好関係
上の選好関係 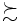 を表現することを考える.
を表現することを考える.
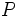 を
を 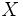 上の確率の全集合とし,
上の確率の全集合とし, 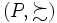 を
を 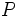 上の選好構造とするとき, 任意の
上の選好構造とするとき, 任意の 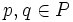 に対して
に対して
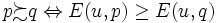
を満たす 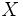 上の基数効用関数
上の基数効用関数 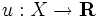 が存在するための必要十分条件は次のように与えられる.
が存在するための必要十分条件は次のように与えられる.
NM1 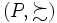 は弱順序である.
は弱順序である.
NM2 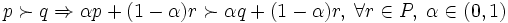
NM3 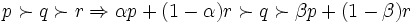 , for some
, for some 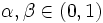
このような 効用関数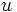 は正線形変換(
は正線形変換(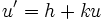 を満たす定数
を満たす定数 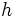 と
と 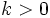 が存在)の範囲で一意であり, 別名フォン・ノイマン=モルゲンシュテルン効用関数という.
が存在)の範囲で一意であり, 別名フォン・ノイマン=モルゲンシュテルン効用関数という.
さらに, サヴェージは, 結果の集合上に客観確率を考える代りに, 自然の集合上に主観確率(subjective probability)を考え, 期待効用最大化の仮説が成り立つ基数効用関数と主観確率が存在するための必要十分条件を求めた. [4]
期待効用仮説に基づく期待効用モデルは, 「決定がいかにあるべきか」を議論する規範的(normative)モデルとしては有用なモデルであるが, 「決定が実際にどのようになされているか」を議論する記述的(descriptive)モデル(あるいは行動科学的モデル)としては問題がある. すなわち, アレーの反例やエルスバーグの反例に見られるように期待効用モデルでは説明できない現象がいくつか存在する [5]. これらを適切に説明するモデルとして, ノーベル経済学賞に輝いたカーネマンとトゥヴァースキによるプロスペクト理論[5]や累積プロスペクト理論[6]が提唱されている.
プロスペクト理論は,期待効用理論における確率を,確率に関する主観的重み付き関数で置き換えて一般化することにより,アレーの判例(確実性効果),希求水準の効果,遊離効果などの,経験的に知られている選好構造を適切に説明するために作られた記述的モデルである.そこで使われる価値関数は,参照点(希求水準)をはさんで利得領域か損失領域で異なり,利得領域における価値は上に凸で緩やかなカーブであるのに対して,損失領域における価値は下に凸で急カーブであり非対称になっている.すなわち,利得領域ではリスク回避型であるのに対して,損失領域ではリスク選好となる.利得と損失の曲線の傾きが異なることは,損失回避を表現している[5].また,確率に関する主観的重み関数は,「人々は非常に小さい確率を,それ自身より大きく感じる」ことをモデル化している.
累積プロスペクト理論も,プロスペクト理論と同様の価値関数を仮定するが,確率に関する重みがプロスペクト理論とは異なっている.すなわち,確率の値が0または1付近の値をとるとき,確率の変化に対する重みの変化が大きく,確率の値が0または1から離れるほど,確率の変化に対する重みの変化が小さくなるようにモデル化されている.これにより,限界感度逓減に関する人々の心理的特性を忠実に表現している.
さらに,期待効用モデルやプロスペクト理論を一般化したリスク下の価値関数や不確実性下の価値関数が提案されていて, そこでは事象の生起確率(またはDempster-Shaferの確率理論 [7] でいう焦点要素の基本確率)も評価属性のひとつとして扱われる [8]. リスク下の価値関数によって,アレーの反例や希求水準の効果はもとより,低確率高損失事象を対象にした期待効用モデルの反例を適切に表現することができる.また,不確実性下の価値関数によって,エルスバーグの反例はもとより,地球環境問題のように不確実性が高くて個々の事象の生起確率を見積もることは困難であるが,事象の集合に対する基本確率を見積もれるような現象を対象にした意思決定支援問題に応用することができる.また,このモデルによって悲観的な選好と楽観的な選好の相違を適切にモデル化することができる.
結果 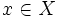 が
が  個の属性
個の属性 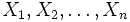 によって特徴づけられているとき, 結果
によって特徴づけられているとき, 結果 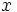 は
は
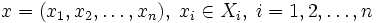
で表される. 起こりうるすべての結果の集合 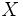 は, 直積集合
は, 直積集合  で表され, これを
で表され, これを  属性空間という.
属性空間という.  属性効用関数は,
属性効用関数は, 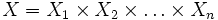 上に
上に ![u:X_1 \times X_2\times \ldots \times X_n \rightarrow [0,1]\,](http://weblio.hs.llnwd.net/e7/img/dict/orjtn/54ca4960688aea1d69ef9d45eb3e831b.png) として定義される. このような
として定義される. このような  属性効用関数を直接求めるには, 複数の属性を同時に考慮して選好判断をしなければならず, 実際にはほとんど不可能である. そこで, 複数の属性間に種々の独立性を仮定して, 直接評価する効用関数の属性の次元を少なくする分解表現を得ることが重要になる. とくに,
属性効用関数を直接求めるには, 複数の属性を同時に考慮して選好判断をしなければならず, 実際にはほとんど不可能である. そこで, 複数の属性間に種々の独立性を仮定して, 直接評価する効用関数の属性の次元を少なくする分解表現を得ることが重要になる. とくに,  個の属性が相互に効用独立という性質を満たすときには, 加法型効用関数
個の属性が相互に効用独立という性質を満たすときには, 加法型効用関数
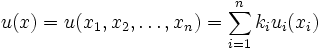
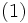
または乗法型効用関数
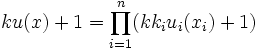
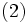
を得ることができる.ただし, ![u_i:X_i \rightarrow [0,1]\,](http://weblio.hs.llnwd.net/e7/img/dict/orjtn/2a7b8805960274560dd4fa4395e7dd49.png) すなわち
すなわち 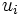 は属性
は属性 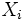 上の効用関数を表す. 分解表現が(1)式のような加法型で表現されるのは,
上の効用関数を表す. 分解表現が(1)式のような加法型で表現されるのは,  個の属性が相互効用独立性はもとより加法独立性という性質を満足するときである. 詳細については文献[9]を参照されたい.
個の属性が相互効用独立性はもとより加法独立性という性質を満足するときである. 詳細については文献[9]を参照されたい.
複数の属性間で効用独立性が満たされないときには属性間に凸依存性という性質を仮定することによりさらに広範囲の分解表現を得ることができる [8].
[1] P.A. Samuelson, Foundations of Economic Analysis, Harvard Univ. Press, Cambridge, USA, 1947. 佐藤隆三訳, 『経済分析の基礎』, 勁草書房, 1967.
[2] 中山弘隆, 谷野哲三, 『多目的計画法の理論と応用』, 計測自動制御学会, 1994.
[3] J. von Neumann and O. Morgenstern, Theory of Games and Economic Behavior Princeton Univ. Press, Princeton, NJ, USA, 1944.
[4] 市川惇信, 『意思決定論』, 共立出版, 1983.
[5] 広田すみれ, 増田真也, 坂上貴之編著:『心理学が描くリスクの世界』, 慶応義塾大学出版会, 2002.
[6] 成川康男, 非線形効用理論・累積プロスペクト理論, 知能と情報(日本知能情報ファジィ学会誌), Vol.16, No.4, pp.296-302, 2004.
[7] G. Shafer, A Mathematical Theory of Evidence, Princeton University Press, Princeton, N. J. 1976.
[8] 田村坦之, 中村 豊, 藤田眞一, 『効用分析の数理と応用』, 計測自動制御学会編, コロナ社, 1997.
[9] R.L. Keeney and H. Raiffa, Decisions with Multiple Objectives, Cambridge Univ. Press (First published by Wiley, New York in 1976), Cambridge, England, 1993.
- こうようかんすうのページへのリンク